Part 2 of 8, Strategies for Integrating the Mathematical Practices into Instruction

By Dr. Michele Douglass

    As with the practice of Reasoning Abstractly and Quantitatively, which was the focus of Part 1 of this series, the practice we will focus on in Part 2 also asks students to reason with mathematics. As I am teaching a class and working to integrate the mathematical practices, I think of these two practices together, even though there are distinct differences. In this blog, we will look specifically at how to get students to Construct Viable Arguments and Critique the Reasoning of Others. I am sure that after you look at these examples, you will see how reasoning is used in two well-defined ways.

    The practice of Constructing Viable Arguments and Critiquing the Reasoning of Others asks students to use and state assumptions, definitions, and previously stated results in their own mathematical arguments. Students should be able to break problems into cases or use counterexamples. They also should be able to compare two plausible arguments to find flaws and explain what has happened. This could be within drawings or diagrams as well as procedures or conceptual explanations. 

    Again, the explanation of the practice is one thing, and the implementation is very different. Here are some classroom examples of problems types that I have used with students. I am including a few notes on the instruction so that you can see how the lessons ask students to either construct viable arguments or critique the reasoning of others.

Example 1:  A big party is taking place, and hexagon tables are being used for seating. The tables are arranged into long rows with one person sitting on each side of the table. The arrangement looks like this:    

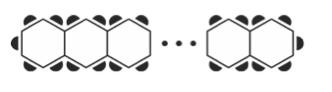
If they can fit 57 tables in a row, how many guests can be seated?  Write an expression to represent the number of guests.

Below is the work of two students.  Which one(s) is/are correct? Why or why not?

                         Student A                                                                          Student B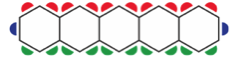                              

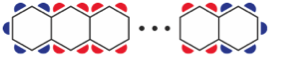
   2(2x57) + 2 = Number of Guests                              4 (57 – 2) + 5 x 2 = Number of Guests

    With just about any content, you can provide student work for your students to critique. Sometimes, the work might be two different approaches to solving a problem. You should have opportunities where there are common errors in work so that students have opportunities to identify these types of errors. Other examples of critiquing work would be in class activities where groups are making decisions. Students are critiquing within the group to form consensus within the group. 

Example 2: I have pennies, nickels, and dimes in my pocket. Suppose I pull out two coins. How much money might I have?

    Not only does this type of a problem lend itself to multiple solutions; it also leads to the conversation about how many different solutions actually exist. When posing this question to students, I know I can push them for justifications, and it always leads to students arguing in a mathematical way about the total number of solutions.

    Think about the questions you can pose.  Are these the only solutions? How do you know? What other methods could be used? Why do you think ___________ method works for finding the total number of unique solutions? Open-ended problems such as this one often provide the opportunity for constructing an argument. 

Example 3: Given the equations below, identify whether it is “Always True,” “Never True,” or “Sometimes True.” Provide examples, counter examples, or solutions to justify your thinking.

A) x + 2 = 3     B) x – 12 = x + 30       C) 2(x + 6) = 2x + 12         D) (x = 4)² = x² + 4²            E) x² + 4 = 0

    One way for students to practice this same type of thinking is to have another set of equations ready with each one on its own “card.” Ask students to work with a partner to sort the cards into groups using these same categories. Have each group justify those that are true by finding all values that make the equation true. To extend the thinking and push students to critique the work of others, have one group compare with another group to form consensus as to the placement of each equation. 

    Think about this third example as a class of instructional lessons. Think about the topics within your grade level where you need to have students understand the classification of items: shapes, equations, graphs, data, etc. When students are classifying, don’t have them stop with placing items into the categories. Have them make justifications as to why the item belongs within that category. Your instruction moves into a much higher rigor when we push students beyond the placement and ask for the justification of the placement. 

    One thing to consider with this particular practice is modeling and setting parameters for healthy and productive classroom discussions. You might consider creating and then using “discussion rules.” Model tone that is appropriate in asking questions and practice if needed. If this is new to you, consider Googling “classroom discourse” for some guidelines on getting started.

    As important as it is to find tasks that involve arguments or critiques, it is equally critical that the teacher pose good questions about the argument or the critique of the work. I find that, by asking these types of questions during lessons, I am modeling for students how to critique the work of others. I am careful with my tone as I ask these questions, especially when I am in a classroom that might not operate in a way that questions student thinking.

• How is youranswer different than ___­­­____’s?
• How can you prove that your answer is correct?
• What math language will help you prove your answer?
• What examples could prove or disprove your argument?
• Will your method still work if _________?
• What do you think about _________’s argument?
• What is the problem with ___­­­­­­______’s thinking?
• Did you try a method that didn’t work?  Why didn’t it work? Would it ever work? Why or why not?
• What questions do you have for _________?
• What might be a nonexample?
• Why do you believe this is true?

References:

Common Core State Standards Initiative Website:  http://www.corestandards.org/Math/Practice/#CCSS.Math.Practice.MP2

Implementing the Mathematical Practice Standards Website: http://mathpractices.edc.org/

Inside Mathematics Website: http://www.insidemathematics.org/index.php/mathematical-practice-standards

Mathematics Assessment Resource Service Website: http://map.mathshell.org/materials/index.php

Michele Douglass, Ph.D., is the president of MD School Solutions, Inc., a company that contracts with school districts on content and pedagogy with teachers and leaders. Her experience ranges from math instructor to director of curriculum and instruction at Educational Testing Services. She has authored several math curricula, as well as professional development and technology programs.